Algorithms and Data Structures
This page is a collection of my notes on stuff that might be helpful in the future.
Currently this is my area of focus so I'll regularly be adding to this page.
Depth First Search (DFS)
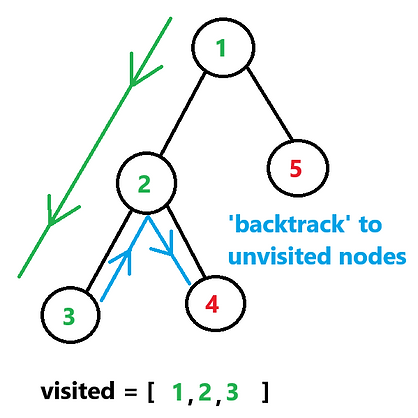
This algorithm is mainly used for searching trees and graphs.
The idea is to follow a brach as far as possible and if tis not found the item then "backtrack" to a node that has a connection to an "unvisited node". This method for search is helpful for solving mazes.
Time complexity: O(V+E)
V = Total Number of vertices / Nodes
E = Total Number of edges / branches
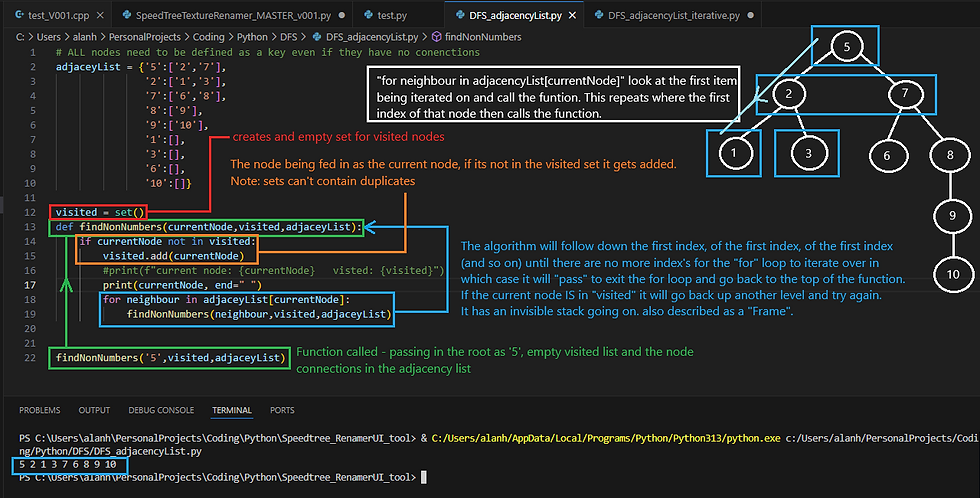
If using a "iterative DFS" approach you will need to use a stack. This will emulate the recursive call stack.
DFS - Recursive Method
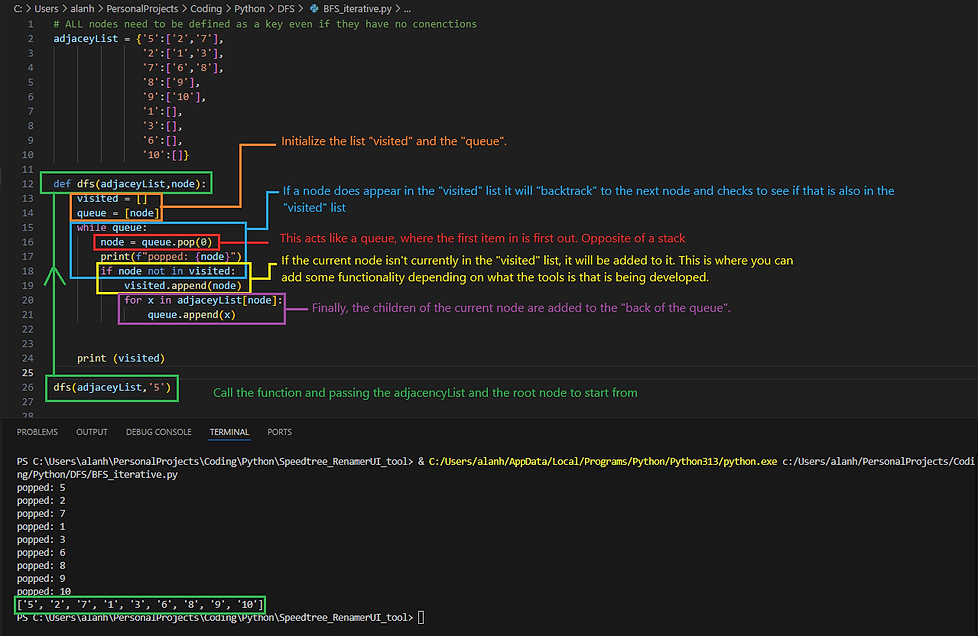
DFS - Iterative Method

Breadth First Search (BFS)
This is different to DFS but uses a very simular technique. Instead of using a "stack" and handeling the most recent entry into the stack, this time a "queue" is used.
There's a few differnt ways to impliment a queue in python but I found the simplest way was to uses a list data structure and use the "pop(0)" method. NOTE that inside the parentheses there is a "0". By default ".pop()" is a stack command but using a 0 means that it will remove the item at the front of the queue (bottom of the stack) acting like "dequeue".
The code is actually identical to DFS - iterative method. The only change is ".pop(0)"
Binary Search
Binary search is an alternative to just iterating over the list / array in a "for" loop.
The standard "for" loop might get lucky and the number that is being searched for could be at the beginning of the list. Alternatively the number could be at the end of the list.
On average it is more likely to be a lot less effecient than a binary search. A binary search needs a 'sorted' list.

A good way to build the functionaily of the binary search is to break the 'min',max' and 'midpoint' of the range out in to variables.
As the search moves through the numbers not only does the midpoint have to get re-calculated but the end ranges need to be updated also.
The 'round()' function is useful to keep numbers as integers, especially if the total range of numbers is odd.
Example:

Modulo and FizzBuzz
Modulo / Modulus is a useful function to be aware of. It returns the remainder of a devision.
Be aware that the Modulo should always return a positive value.
Dividend = Divisior * Quotient + Remainder
For example
0 Mod 5 = ERROR: can't divide by zero
1 Mod 5 = 1
2 Mod 5 = 2
3 Mod 5 = 3
4 Mod 5 = 4 (5 doesn't fully divide 4 so the remainder is 4)
5 Mod 5 = 0 (no remainder when 5 is divided by itself)
6 Mod 5 = 1 (5 does dived fully into 6 once and has a remainder of 1)
7 Mod 5 = 2
8 Mod 5 = 3
9 Mod 5 = 4
10 Mod 5 = 0 (5 fully divieds into 10 twice with no remainder so the result is 0)
11 Mod 5 = 1
Notive a repaeating sqencing pattern. This can be useful to draw shapes or animted when mixed with time.
TIP: To sort odd and even numbers using "Mod2" will give a binary/boolean result.
Modulo on Negative Numbers
You can perform modulo function on negative numbers but I found for myself i have to think about it slightly differntly.
6 Mod 5 = 4
a Mod b = c
The remainder still needs to be a positive number so to achive this go for the smallest multiple number of (b) that can the negative number (a) can divide into that will give a positive remainder. In this case its -10.
Quotient * Divisor + Remainder = Dividend
-2 * 5 + 4 = -6
Solving FizzBuzz using Modulo
A common programming challenge is FizzBuzz
given a list of integers print:
- “Fizz” if the integer is divisible by 3
- “Buzz” if the integer is divisible by 5
- “FizzBuzz” if the integer is divisible by 3 and 5
Recursion
A recursive algorithm uses functions that call themselves to solve a problem that depends on smaller instances of the same problem. Recursion can be a powerful tool for writing algorithms, and is used in problems like merge sort and tree traversal.
"!" represents factorial.
4! = 4*3*2*1 or 4!= 4 *3!
which can be written as:
n! = n*(n-1)!
Recursive function calls occur when the function calls itself.
Be aware that you can end up in a endless loop if a "base case" isn't set.
A "base case" is a value that is the condition to exit the loop.
Depending on the language used recursion can be singniicatly slower with more memory overhead that just iteration, like Python, Java and potenailly C. In functional languages "For" loops can be more expensive.
